循环赛日程表问题报告

先来想想问题的约束条件

我们要输出这么一张表

  • 如果n是奇数，则表是n行n列的，第j列包含除去j以外的所有从1到n的数字，除此之外还包括一个0（表示不参赛）。同一行中一个数字最多只能出现一次，可以不出现。
  • 如果n是偶数，则表是n-1行n列的，第j列包含除去j以外的所有从1到n的数字。同一行中一个数字最多只能出现一次，可以不出现。

我们先考虑一下分治怎么做。特殊情况下例如n为2的次幂的做法，我们已经在课堂上学过了。我们唯一要解决的是遇到奇数怎么办。很显然，对于奇数子问题，每天都会有一个人可以休息，不需要打比赛，为了让问题可以使用相近的办法处理，我们很容易的就想到了引入一个虚拟的玩家来陪这个人玩的方法。很显然这个引入的虚拟玩家不会在一天之内重复比赛，也不会与某个人重复多次比赛。仍然满足循环赛的性质。剩下的就和课堂上学的普通循环赛做法差不多了。

分析一波复杂度。递归$\log{N}$次，每次copy来copy去的与$N^2$同阶。总复杂度$O(N^2\log{N})$。

emmm，可是这张表的大小才$N^2$这么大啊，我们不能把这个$\log{N}$给去掉吗？可是只要我们进行分治，并且每次都要copy的话，这个复杂度肯定就下不来。去掉copy部分？好像有点难。

不过我们何必局限于分治呢？我们直接想其他办法逼近下届$(N^2)$不好么？

通过画图，我发现一个很棒的性质。对于奇数个玩家，如果把他们画成一个圈，遍历每个玩家，所产生的角点反射，正好构成了一个符合循环赛性质的置换集合。

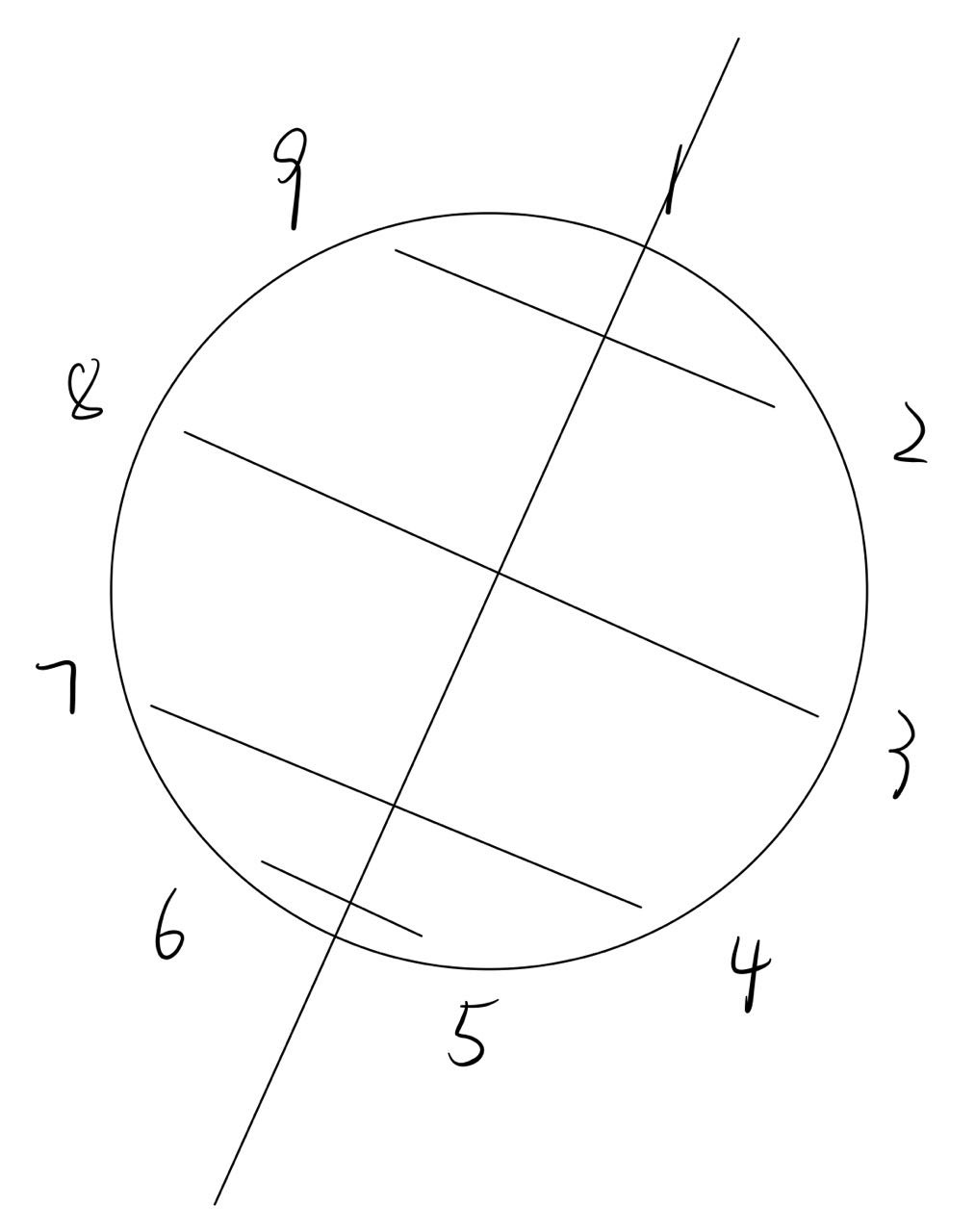
image_82.png
以1为角的角点反射

应用这个性质，我们很快就能够写出第一版，只支持计数的循环赛日程安排程序。

我们再考虑n为偶数的时候，我们还能够应用和刚刚类似的方法去进行日程安排吗？

很遗憾，不能。

n为偶数的时候，总共有2n种反射方案，这2n种方案显然要进行一定的筛选才有可能生成一个可行的解，别扭不优雅。我们可以换种思路，结合一下分治做法当中引入虚拟玩家的思想，我们把偶数个的合法玩家中的一个先给踢出去，一会再想办法给他弄回来。这样问题就转化成为了在奇数个玩家种安排日程表的问题了，是我们刚刚已经解决的问题，我们可以套用那个算法。

好，现在我们考虑如何把刚刚踢出去的玩家再给弄回来。奇数情况下的算法中，每个人至少会休息一天，那天没人和他比赛，那我们不妨让这个被踢出去的玩家在那些天比赛。由于这些0在一列当中只出现一次，在一行当中也只出现一次，把他替换成我们刚刚踢出去的玩家并不会破坏循环赛的性质，我们就给他加进去好了。

emmm，问题好像就这么解决了？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
#define MXN 107
using namespace std;

int n, days;
int arr[MXN * 3];
int vs[MXN][MXN];
void work(int n) {
    days = (n & 1) ? n : n - 1;
    for (int i = 0; i < days; ++i) {
        arr[i] = arr[i + days] = arr[i + days * 2] = i + 1;
    }
    for (int i = 0; i < days; ++i) {
        for (int j = 1; j <= days / 2; ++j) {
            vs[i][arr[days + i - j]] = arr[days + i + j];
            vs[i][arr[days + i + j]] = arr[days + i - j];
        }
    }
    if ((n & 1) == 0) {
        for (int i = 0; i < days; ++i) {
            vs[i][i + 1] = n;
            vs[i][n] = i + 1;
        }
    }
}

int main() {
    scanf("%d", &n);
    work(n);
    printf("Player : ");
    for (int i = 1; i <= n; ++i) {
        printf("%4d", i);
    }
    putchar('\n');
    for (int i = 0; i < days; ++i) {
        printf("Day #%2d: ", i + 1);
        for (int j = 1; j <= n; ++j) {
            printf("%4d", vs[i][j]);
        }
        putchar('\n');
    }
}